### 题目描述 我们有 n 栋楼,编号从 0 到 n - 1 。每栋楼有若干员工。由于现在是换楼的季节,部分员工想要换一栋楼居住。 给你一个数组 requests ,其中 requests[i] = [fromi, toi] ,表示一个员工请求从编号为 fromi 的楼搬到编号为 toi 的楼。 一开始 所有楼都是满的,所以从请求列表中选出的若干个请求是可行的需要满足 每栋楼员工净变化为 0 。意思是每栋楼 离开 的员工数目 等于 该楼 搬入 的员工数数目。比方说 n = 3 且两个员工要离开楼 0 ,一个员工要离开楼 1 ,一个员工要离开楼 2 ,如果该请求列表可行,应该要有两个员工搬入楼 0 ,一个员工搬入楼 1 ,一个员工搬入楼 2 。 请你从原请求列表中选出若干个请求,使得它们是一个可行的请求列表,并返回所有可行列表中最大请求数目。 ### 输入输出 #### 示例1 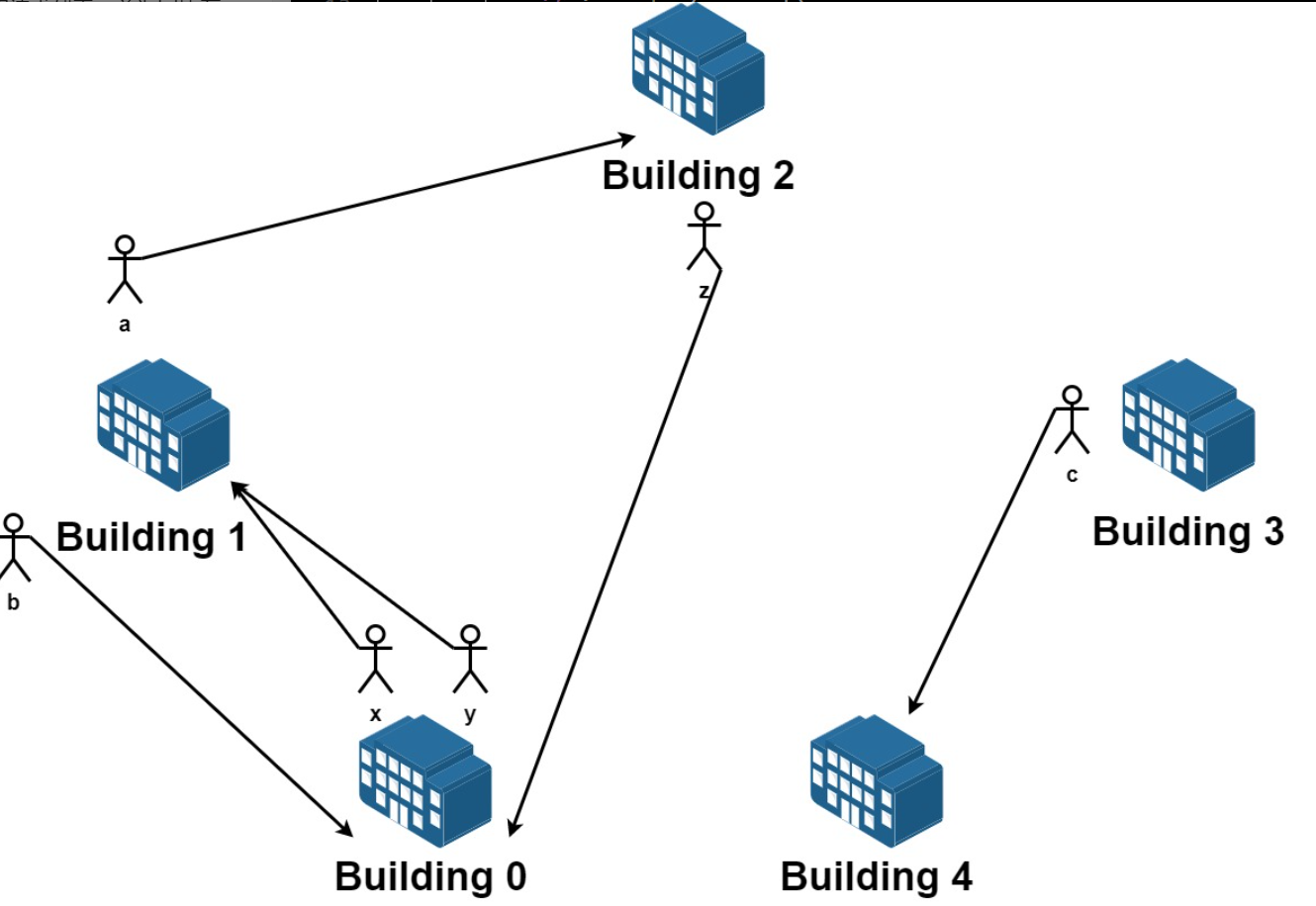 ``` 输入:n = 5, requests = [[0,1],[1,0],[0,1],[1,2],[2,0],[3,4]] 输出:5 解释:请求列表如下: 从楼 0 离开的员工为 x 和 y ,且他们都想要搬到楼 1 。 从楼 1 离开的员工为 a 和 b ,且他们分别想要搬到楼 2 和 0 。 从楼 2 离开的员工为 z ,且他想要搬到楼 0 。 从楼 3 离开的员工为 c ,且他想要搬到楼 4 。 没有员工从楼 4 离开。 我们可以让 x 和 b 交换他们的楼,以满足他们的请求。 我们可以让 y,a 和 z 三人在三栋楼间交换位置,满足他们的要求。 所以最多可以满足 5 个请求。 ``` #### 示例2 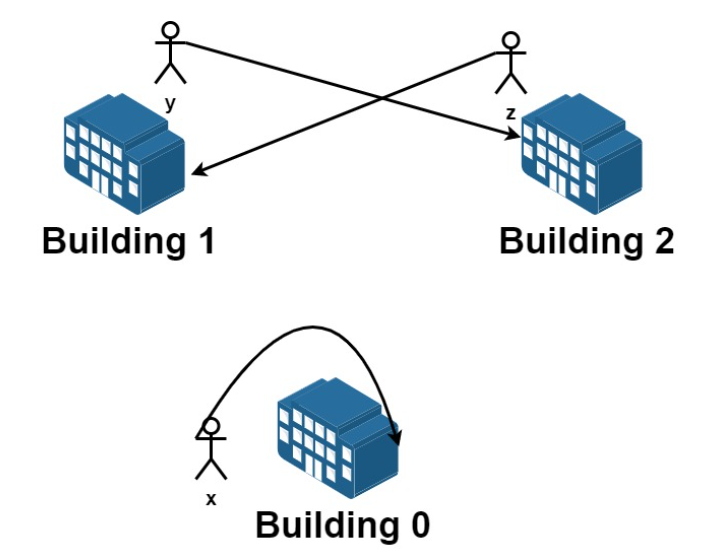 ``` 输入:n = 3, requests = [[0,0],[1,2],[2,1]] 输出:3 解释:请求列表如下: 从楼 0 离开的员工为 x ,且他想要回到原来的楼 0 。 从楼 1 离开的员工为 y ,且他想要搬到楼 2 。 从楼 2 离开的员工为 z ,且他想要搬到楼 1 。 我们可以满足所有的请求。 ``` **提示:** - 1 <= n <= 20 - 1 <= requests.length <= 16 - requests[i].length == 2 - 0 <= fromi, toi < n ### 题目思路 对于该问题,我们注意给的数据范围是比较小的。请求的数量最大为**16**,每个请求只有接受和拒绝这2种选项,因此枚举所有可能共$$2^{16}=65536$$种可能,采用枚举是可以接受的做法。 #### 思路1 采用回溯的方式,每次枚举2种可能性,如果在枚举的过程中发现该方式可接受的请求大于最大请求,将其记录。 **算法复杂度** 假设房子的数量为m,请求数量为n 时间复杂度:枚举接受所有请求的可能共$$O(2^n)$$, 对每种可能性检查m个房子的移动人数是否全0,复杂度共$$O(2^nm)$$ 空间复杂度:采用回溯法,栈的深度与请求序列的深度相同,空间复杂度$$O(n)$$ #### 思路2 通过二进制的方式进行枚举,对于n个请求,采用$$[0,2^n)$$对n个请求进行枚举。 时间复杂度:枚举接受所有请求的可能共$$O(2^n)$$, 对每种可能性检查m个房子的移动人数是否全0,复杂度共$$O(2^nm)$$ 空间复杂度:采用回溯法,栈的深度与请求序列的深度相同,空间复杂度$$O(n)$$ **算法复杂度** 假设房子的数量为m,请求数量为n 时间复杂度:枚举接受所有请求的可能共$$O(2^n)$$, 对每种可能性检查m个房子的移动人数是否全0,复杂度共$$O(2^nm)$$ 空间复杂度:每次检查时查看房子的人数,空间复杂度$$O(m)$$ #### 代码实现1 ```python class Solution: def __init__(self): self.move_people = None # 每栋楼移动人数为0 self.request_li = None self.request_num = 0 self.max_req = 0 def maximumRequests(self, n: int, requests: List[List[int]]) -> int: def dfs(request: List[List[int]], i: int): if i == len(request): return # 分支1 接受该请求 self.move_people[request[i][0]] = self.move_people[request[i][0]] - 1 self.move_people[request[i][1]] = self.move_people[request[i][1]] + 1 self.request_li[i] = True self.request_num = self.request_num + 1 zero = True for peo in self.move_people: if peo != 0: zero = False break if zero and self.request_num > self.max_req: self.max_req = self.request_num dfs(request, i+1) self.move_people[request[i][0]] = self.move_people[request[i][0]] + 1 self.move_people[request[i][1]] = self.move_people[request[i][1]] - 1 self.request_li[i] = False self.request_num = self.request_num - 1 # 分支2 拒绝该请求 dfs(request, i+1) self.move_people = [0] * n # 每栋楼移动人数为0 self.request_li = [False] * len(requests) dfs(requests, 0) return self.max_req ``` #### 代码实现2 ```python def getbits(self, num: int): count = 0 for i in range(32): if (num >> i) & 1 == 1: count = count + 1 return count def maximumRequests(self, n: int, requests: List[List[int]]) -> int: res = 0 for mask in range(2 ** len(requests)): request_num = self.getbits(mask) if request_num <= res: continue move_people = [0] * n for i in range(len(requests)): if (mask >> i) & 1 == 1: move_people[requests[i][0]] -= 1 move_people[requests[i][1]] += 1 zeros = True for i in range(n): if move_people[i] != 0: zeros = False break if zeros and request_num > res: res = request_num return res ``` 最后编辑:2024年04月23日 ©著作权归作者所有 赞 0 分享
最新回复